|
About SAT Exam
Multiple Choice Questions
Information
The questions that follow will give you an idea of the type of mathematical thinking required to solve problems on the SAT. First, try to answer each question yourself, and then read the solutions that follow. These solutions may give you new insights into solving the problems or point out techniques you'll be able to use again. Most problems can be solved in a variety of ways, so don't be concerned if your method is different from the one given. Note that the directions indicate that you are to select the best of the choices given.
Directions
For this section, solve each problem and decide which is the best of the choices given. Fill in the corresponding circle on the answer sheet. You may use any available space for scratchwork.
Notes
1. The use of a calculator is permitted.
2. All numbers used are real numbers.
3. Figures that accompany problems in this test are intended to provide information useful in solving problems.
4. They are drawn as accurately as possible EXCEPT when it is stated in a specific problem that the figure is not drawn to scale. All figures lie in a plane unless otherwise indicated.
5. Unless otherwise specified, the domain of any function is assumed to be the set of all real numbers x for which (x) is a real number.
Reference Information
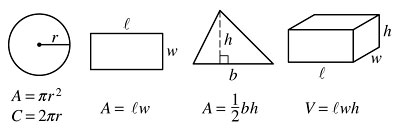
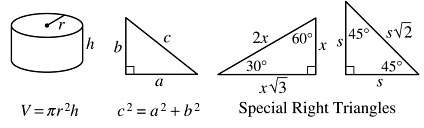
The number of degrees of arc in a circle is 360.
The sum of the measures in degrees of the angles of a triangle is 180.
Multiple Choice
A special lottery is to be held to select the student who will live in the only deluxe room in a dormitory. There are 100 seniors, 150 juniors, and 200 sophomores who applied. Each senior's name is placed in the lottery 3 times; each junior's name, 2 times; and each sophomore's name, 1 time. What is the probability that a senior's name will be chosen?
(A) 1/8
(B) 2/9
(C) 2/7
(D) 3/8
(E) 1/2
Explanation:
Correct Answer: D
To determine the probability that a senior's name will be chosen, you must determine the total number of seniors' names that are in the lottery and divide this number by the total number of names in the lottery. Since each senior's name is placed in the lottery 3 times, there are 3 Χ 100 = 300 seniors' names. Likewise, there are 2 Χ 150 = 300 juniors' names and 1 Χ 200 = 200 sophomores' names in the lottery. The probability that a senior's name will be chosen is .
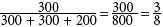
|