|
About ACT Exam
Mathematics Answer Key
1. The correct answer is B.
By definition, x4 means the product of 4 factors of x so x4 is
equivalent to (x)(x)(x)(x).
A.
4x = x + x + x + x, which is not the same as the
product of 4 factors of x.
C. x + 4 is not the same as the product of 4 factors of x.
D. 4 x is x factors of 4, which is not the
same as the product of 4 factors of x.
E. 2x2 is 2  x x  x, which is not the
same as the product of 4 factors of x. x, which is not the
same as the product of 4 factors of x.
2. The correct answer is K.
The rectangle is 3 inches by
6 inches, so the area is 3(6) = 18 square inches.
F.
If
the area were 6, then l = 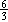 = 2, but this length isn't twice
the width. = 2, but this length isn't twice
the width.
G. If the area were 9, then l = 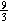 = 3, but this length
isn't twice the width. = 3, but this length
isn't twice the width.
H. If the area were 12, then l =  = 4, but this length
isn't twice the width. = 4, but this length
isn't twice the width.
J. If the area were 15, then l = 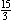 = 5, but this length
isn't twice the width. = 5, but this length
isn't twice the width.
3. The correct answer is A.
There are 14 balloons, of
which 9 are yellow. If a yellow balloon is sold, there are 13 balloons left, of
which 8 are yellow. The probability of selecting a yellow balloon is 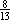 . .
B.
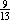 cannot
be the probability of selecting a yellow balloon; cannot
be the probability of selecting a yellow balloon; 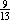  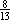 because 9(13) because 9(13) 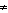 8(13). 8(13).
C. 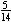 cannot be the probability of
selecting a yellow balloon; cannot be the probability of
selecting a yellow balloon; 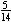 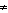 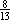 because 5(13) = 65, 14(8) = 112,
and 65 because 5(13) = 65, 14(8) = 112,
and 65 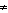 112. 112.
D. 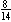 cannot be the probability of
selecting a yellow balloon; cannot be the probability of
selecting a yellow balloon; 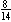 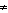 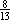 because 8(13) because 8(13) 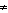 8(14). 8(14).
E. 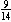 cannot be the probability of
selecting a yellow balloon; cannot be the probability of
selecting a yellow balloon; 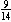 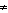 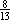 because 9(13) = 117, 14(8) = 112,
and 117 because 9(13) = 117, 14(8) = 112,
and 117 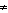 112. 112.
4. The correct answer is J.
3  10- 4 = 3 10- 4 = 3  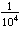 = 3 = 3   =
0.0003 =
0.0003
F.
-30,000 in scientific notation is -3  104, not 3 104, not 3  10-
4. 10-
4.
G. -120 in scientific notation is -1.2  102, not 3 102, not 3  10-
4. 10-
4.
H. 0.00003 in scientific notation is 3  10- 5, not 3 10- 5, not 3  10-
4. 10-
4.
K. 0.12 in scientific notation is 1.2  10-1, not 3 10-1, not 3  10-
4. 10-
4.
5. The correct answer is C.
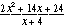 = = 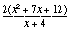 = = 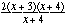 = 2(x + 3) = 2(x + 3)
A.
If 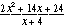 simplifies
to x + 3, then both should have the same value for all x > 0.
But if x = 1, simplifies
to x + 3, then both should have the same value for all x > 0.
But if x = 1, 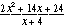 = = 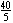 = 8 and x + 3 = 1
+ 3 = 4. = 8 and x + 3 = 1
+ 3 = 4.
B.
If 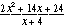 simplifies
to x + 4, then both should have the same value for all x > 0.
But if x = 1, simplifies
to x + 4, then both should have the same value for all x > 0.
But if x = 1, 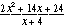 = = 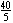 = 8 and x + 4 = 1
+ 4 = 5. = 8 and x + 4 = 1
+ 4 = 5.
D.
If 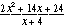 simplifies
to 2(x + 4), then both should have the same value for all x >
0. But if x = 1, simplifies
to 2(x + 4), then both should have the same value for all x >
0. But if x = 1, 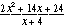 = = 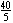 = 8 and 2(x + 4) =
2(1 + 4) = 10. = 8 and 2(x + 4) =
2(1 + 4) = 10.
E.
If 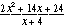 simplifies
to 2(x + 3)(x + 4), then both should have the same value for all x > 0. But if x = 1, simplifies
to 2(x + 3)(x + 4), then both should have the same value for all x > 0. But if x = 1, 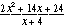 = = 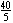 = 8 and 2(x + 3)(x + 4) = 2(4)(5) = 40. = 8 and 2(x + 3)(x + 4) = 2(4)(5) = 40.
6. The correct answer is F.
By the Pythagorean theorem,
the length of the hypotenuse is 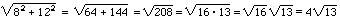 . .
G.
 is the
hypotenuse of a right triangle with legs 12 and 4, since is the
hypotenuse of a right triangle with legs 12 and 4, since 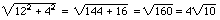 ; so ; so  can't
be the hypotenuse of a right triangle with legs 12 and 8. can't
be the hypotenuse of a right triangle with legs 12 and 8.
H.
 can't
be the hypotenuse because is would be the shortest side of the triangle. can't
be the hypotenuse because is would be the shortest side of the triangle.
J.
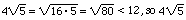 can't
be the hypotenuse because it would be shorter than one of the legs. can't
be the hypotenuse because it would be shorter than one of the legs.
K.
4
< 8, so 4 can't be the hypotenuse because it would be the shortest side of
the triangle.
7. The correct answer is D.
Since circles have equations
of the form (x - h)2 + (y - k)2 = r2,
for the given circle, r2 = 9, so r = 3.
Then A =  r2 = r2 =  (3)2 = 9 (3)2 = 9 . .
A.
A
circle with area 3 has radius has radius 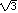 , since , since  ( (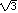 )2 =
3 )2 =
3 ; ;
but the radius of the given circle is 3, not 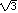 . .
B. A circle with area 4 has radius 2, since has radius 2, since  (2)2 =
4 (2)2 =
4 ;
but the radius of the given circle is 3, not 2. ;
but the radius of the given circle is 3, not 2.
C. A circle with area 6 has radius has radius 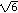 , since , since  ( (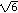 )2 =
6 )2 =
6 ;
but the radius of the given circle is 3, not ;
but the radius of the given circle is 3, not 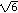 . .
E. A circle with area 16 has radius 4, since has radius 4, since  (4)2 =
16 (4)2 =
16 ;
but the radius of the given circle is 3, not 4. ;
but the radius of the given circle is 3, not 4.
8. The correct answer is H.
x
2
- 15
= 0, so x2 = 15, x = ?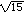 . .
If x = -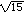 , x2 - 15 = (- , x2 - 15 = (-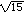 )2 - 15 = 15 - 15 = 0. )2 - 15 = 15 - 15 = 0.
If x = 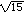 , x2 - 15 = ( , x2 - 15 = (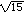 )2 - 15 = 15 - 15 = 0. )2 - 15 = 15 - 15 = 0.
Thus both -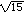 and and 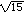 satisfy the equation, so
there are two solutions. satisfy the equation, so
there are two solutions.
F
and G
are
not correct because two numbers have been shown to satisfy the equation.
J and K are not correct because a quadratic equation has at most two
solutions.
9. The correct answer is B.
If the circle with center
(-3,4) is tangent to the x-axis, the point of tangency is (-3,0) and the
distance between these points is 4, so the radius is 4.
A.
If r = 3, the equation of the circle is (x + 3)2 + (y - 4)2 = 9.
This circle is tangent to the x-axis so it contains a point for which y = 0.
But then (x + 3)2 + (0 - 4)2 = 9, (x + 3)2 + 16 = 9, (x + 3)2 = -7, which is impossible since squares
can't be negative.
C.
If r = 5, the equation of the circle is (x + 3)2 + (y - 4)2 = 25.
When y = 0, (x + 3)2 + (0 - 4)2 = 25, (x + 3)2 + 16 = 25, (x + 3)2 = 9, x + 3 = ?3, x = 0, -6.
So this circle crosses the x-axis at (0,0) and (-6,0) and is not tangent
to the x-axis.
D.
If r = 9, the equation of the circle is (x + 3)2 + (y - 4)2 = 81.
When y = 0, (x + 3)2 + (0 - 4)2 = 81, (x + 3)2 + 16 = 81, (x + 3)2 = 65, x + 3 = ?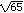 , x = -3 ? , x = -3 ? 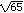 . .
So this circle crosses the x-axis at (-3 - 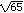 ,0) and (-3 + ,0) and (-3 + 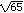 ,0) and
is not tangent to the x-axis. ,0) and
is not tangent to the x-axis.
E.
If r = 16, the equation of the circle is (x + 3)2 + (y - 4)2 = 256.
When y = 0, (x + 3)2 + (0 - 4)2 = 256, (x + 3)2 + 16 = 256, (x + 3)2 = 240, x + 3 = ?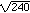 , x = -3 ? , x = -3 ? 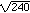 . .
So this circle crosses the x-axis at (-3 - 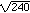 ,0) and (-3 + ,0) and (-3 + 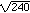 ,0) and
is not tangent to the x-axis. ,0) and
is not tangent to the x-axis.
10. The correct answer is F.
Since sin2A + cos2A = 1, ( )2 + cos2A = 1, cos2A = 1 - )2 + cos2A = 1, cos2A = 1 - 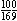 , cos2A = , cos2A =  , so
cosA = ? , so
cosA = ?  = ? = ? 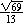 . .
But since 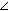 A is acute, cosA = A is acute, cosA = 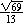 . .
G.
( )2 + ( )2 + (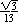 )2 = )2 = 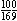 + + 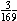 = = 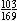 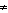 1, so
cosA 1, so
cosA 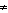 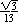 . .
H. ( )2 + ( )2 + (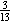 )2 = )2 = 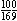 + + 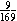 = = 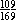 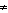 1, so
cosA 1, so
cosA 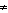 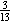 . .
J. ( )2 + ( )2 + (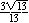 )2 = )2 = 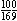 + + 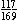 = = 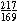  1, so
cosA 1, so
cosA 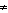 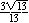 . .
K. ( )2 + ( )2 + (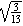 )2 = )2 = 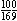 + + 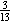 = =  = =  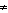 1, so
cosA 1, so
cosA 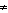 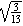 . .
11. The correct answer is A.
If a|b - 2|
< 0, one of a or |b - 2| must be negative and one must be
positive.
Since |b - 2| can't be negative, a must be negative. Then |b - 2| must be positive, so b 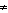 2. 2.
B.
If b = 2, |b - 2| = 0 and a|b - 2| = 0, but 0 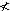 0. 0.
C. The values a = 1 and b = 3 meet the conditions a 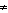 0
and b > 2, 0
and b > 2,
but a|b - 2| = 1|3 - 2| = 1  1 = 1, and 1 1 = 1, and 1 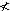 0. 0.
D. The values a = 1 and b = 1 meet the conditions a > 0 and b < 2,
but a|b - 2| = 1|1 - 2| = 1  1 = 1, and 1 1 = 1, and 1 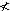 0. 0.
E. Values of a and b do exist for which a|b - 2| < 0.
For example, if a = -1 and b = 3, a|b - 2| = (-1)|3
- 2| = -1  1 = -1, and -1 < 0. 1 = -1, and -1 < 0.
12. The correct answer is G.
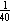 of 1,000 light bulbs were
defective, so of 1,000 light bulbs were
defective, so 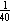 (1,000) or 25 bulbs were defective. (1,000) or 25 bulbs were defective.
The rest, 1,000 - 25 or 975, were nondefective. The ratio of defective to
nondefective is 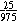 = = 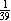 . .
F.
If
the ratio of defective bulbs to nondefective bulbs were 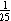 , then out of every 26
bulbs, 1 would be defective, so , then out of every 26
bulbs, 1 would be defective, so 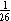 of the bulbs would be defective.
But the fraction of defective bulbs is of the bulbs would be defective.
But the fraction of defective bulbs is 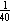 . .
H. If the ratio of defective bulbs to nondefective bulbs were 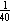 , then
out of every 41 bulbs, 1 would be defective, so , then
out of every 41 bulbs, 1 would be defective, so 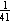 of the bulbs would be
defective. But the fraction of defective bulbs is of the bulbs would be
defective. But the fraction of defective bulbs is 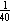 . .
J. If the ratio of defective bulbs to nondefective bulbs were 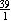 , then
out of every 40 bulbs, 39 would be defective, so , then
out of every 40 bulbs, 39 would be defective, so 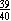 of the bulbs would be
defective. But the fraction of defective bulbs is of the bulbs would be
defective. But the fraction of defective bulbs is 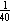 . .
K. If the ratio of defective bulbs to nondefective bulbs were 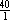 , then
out of every 41 bulbs, 40 would be defective, so , then
out of every 41 bulbs, 40 would be defective, so  of the bulbs would be
defective. But the fraction of defective bulbs is of the bulbs would be
defective. But the fraction of defective bulbs is 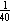 . .
|